Interdisciplinary Research
My primary research interest is advancing data-driven decision-making under uncertainty, with a particular focus on two-stage stochastic optimization. My approach balances theoretical novelty with application-driven impact, addressing complex societal and environmental challenges through the creative development of mathematical models. These models are often large-scale, typically requiring the design of specialized algorithms to enable computationally efficient solutions.
One central focus of my research is chance-constrained optimization, where the goal is to design systems that remain resilient even under extreme risk conditions. I work on developing specialized algorithms to solve such stochastic programs, ensuring both tractability and practicality. A second recurring theme is the development of new axiomatic definitions of fairness. Here, I seek to design continuous or discrete optimization models whose Karush–Kuhn–Tucker (KKT) optimality conditions lead to these fairness notions.
Some agencies funding my research are:

Motivations and Applications
My work is inherently interdisciplinary, driven by real-world challenges such as:
- Energy Systems: Designing resilient and sustainable energy infrastructures under uncertain demand and supply.
- Pandemic Response: Guiding healthcare policy to ensure fairness across populations and allocate scarce resources effectively.
- Critical Risk Management: Minimizing the socioeconomic impact of unforeseen man-made attacks or natural disasters.
- Sustainable Waste Management: Developing models for the efficient placement of recycling centers to promote environmental sustainability.
A unique aspect of my approach is modeling subjective human behavior within the decision-making process. This adds both complexity and realism to my models, bridging the gap between mathematical rigor and human-centric decision-making.
Probabilistic Bounds
This research represents a purely theoretical interest, in which I explore joint-chance constraints through the lens of classical probability theory. Specifically, I approach a joint-chance constraint as a union of sets and utilize classical probability bounds to constrain it effectively. Bounding the probability of the union of n events using joint probabilities of k < n events has a rich history, dating back to the foundational work of Boole and Bonferroni.
What makes this line of probabilistic research particularly interesting is its application in optimization models. When these probabilistic bounds are incorporated into chance-constrained optimization models, they provide upper and lower bounds on the optimal objective function value, offering both computational and theoretical insights. [Click for more →]
Explore →
Sustainability & Climate Change
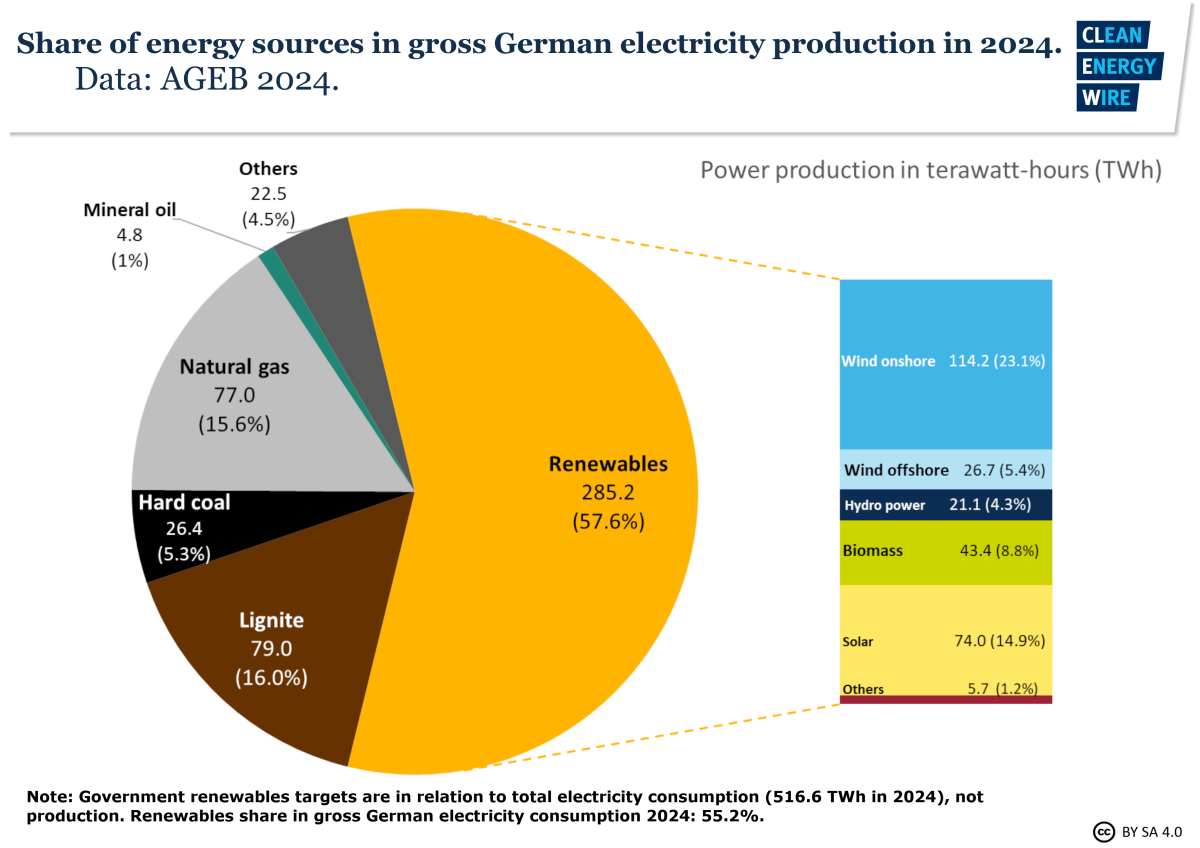
As several countries advance towards Net-Zero goals (e.g., Germany's Energiewende or France's Transition Énergétique), joint chance constraints have proven especially effective for ensuring highly reliable operation of critical energy systems under uncertain renewable energy availability, such as photovoltaic (PV) systems and coupled wind–diesel systems. Mathematical optimization models for such systems often present significant challenges due to their (a) structure and (b) scale, necessitating the development of heuristics and algorithms.
My research has designed modern machine learning-inspired iterative algorithms and employed Lagrangian-based proximal terms to tackle these challenges. See this older article and this newer article. [Click for more →]
Fairness & Waste Management
In 2020, I began exploring undesirable facility location problems (FLPs) with a unique perspective: ensuring fairness from the point of view of the facilities, rather than the users, which is the typical approach in existing literature. Motivated by applications in waste management, particularly in the context of recycling centers (e.g., UK tips or German Wertstoffhöfe), I lead a diverse team of researchers on this subtopic.
Supported by the Bavarian State Ministry for Science & Arts and the University of Southampton, my team develops discrete optimization models that achieve fairness in facility closures. So far this effort has led to:
- Three student theses with three published articles.
- Grant funding supporting a postdoctoral researcher to quantify subjective opinions on recycling campaigns and incorporate human perceptions into decision models. [Click for more →]
Explore →

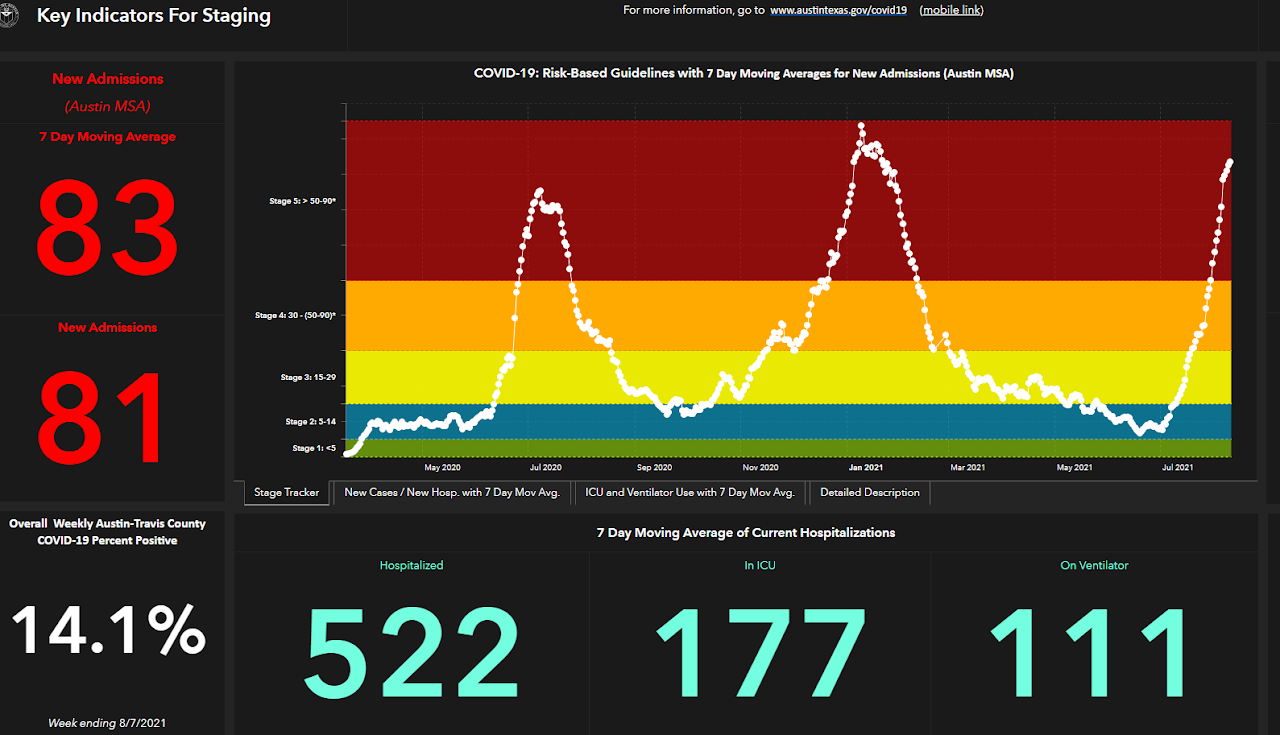
Pandemic Risk Mitigation
I began collaborating with the Texas Department of State Health Services, US, as an MSc student in 2012, helping prepare for future pandemics long before the emergence of COVID-19. Motivated by Texas's response to the 2009 H1N1 pandemic, my PhD research focused on designing web-based, optimization-backed decision-support tools for government use. These tools, accessible at flu.tacc.utexas.edu, assist the State of Texas in the fair and efficient allocation of critical resources, such as antivirals and vaccines.
The most significant funding here is provided by a three-year grant from the Deutsche Forschungsgemeinschaft (German Research Foundation), with additional funding from the Bavarian Czech Academic Agency and the EU Horizon 2020 Program. [Click for more →]
Explore →